Ngân hàng bài tập
SS
Cho hàm số $y=f(x)$ có bảng biến thiên như hình vẽ sau:
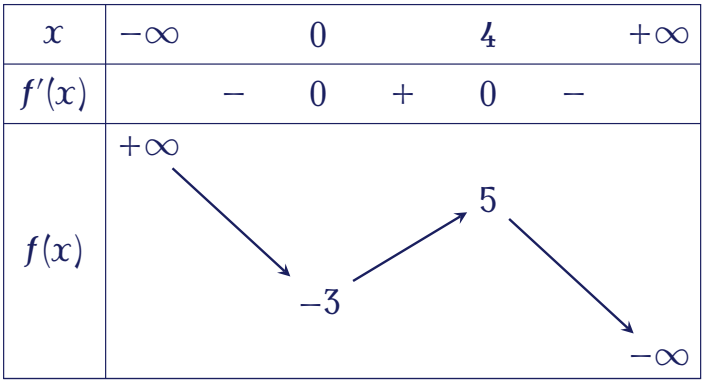
Giá trị lớn nhất của hàm số $g(x)=f\big(4x-x^2\big)+\dfrac{x^3}{3}-3x^2+8x+\dfrac{1}{3}$ trên đoạn $[1;3]$ bằng
| $15$ | |
| $\dfrac{25}{3}$ | |
| $\dfrac{19}{3}$ | |
| $12$ |
1 lời giải
Chọn phương án D.
Ta có $\begin{aligned}[t]
g'(x)&=(4-2x)f'\big(4x-x^2\big)+x^2-6x+8\\
&=2(2-x)f'\big(4x-x^2\big)+(x-2)(x-4)\\
&=(2-x)\left[2f'\big(4x-x^2\big)+4-x\right].
\end{aligned}$
Trên đoạn $[1;3]$ ta có:
- $x<4\Rightarrow4-x>0$ (1)
- Đặt $u=4x-x^2$. Dễ thấy $u\in[3;4]$.
Dựa vào bảng biến thiên ta thấy $f'(u)>0$ (2)
Từ (1) và (2) suy ra $2f'\big(4x-x^2\big)+4-x=2f'(u)+4-x>0$ với $\forall x\in[1;3]$.
Xét dấu $g'(x)$:
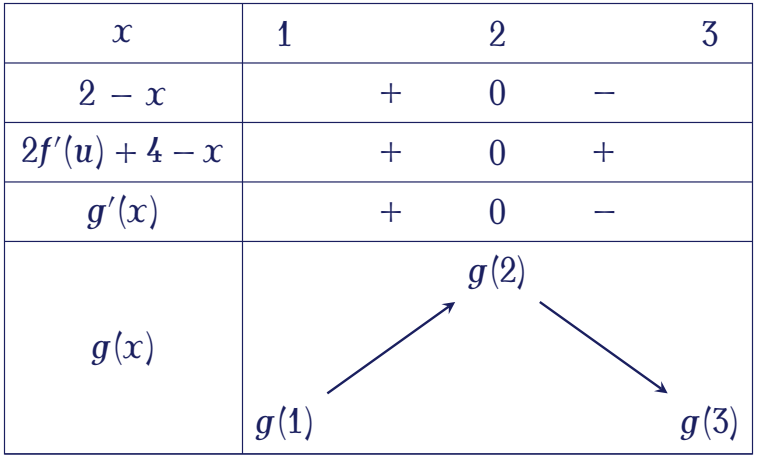
Vậy giá trị lớn nhất của $g(x)$ trên đoạn $[1;3]$ bằng $$\begin{aligned}
g(2)&=f\big(4\cdot2-2^2\big)+\dfrac{2^3}{3}-3\cdot2^2+8\cdot2+\dfrac{1}{3}\\
&=f(4)+7\\
&=5+7=12.
\end{aligned}$$
