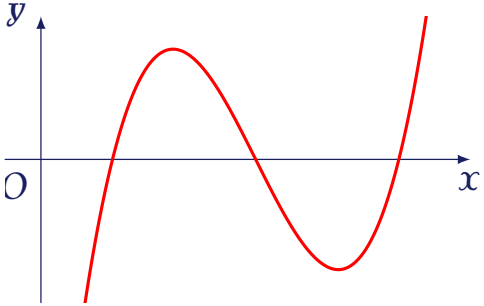
Cho hàm số $f(x)=ax^3+bx^2+cx+d$ ($a\neq0$) có đồ thị là đường cong trong hình bên.
Số các giá trị nguyên của tham số $m\in(-2019;2023]$ để phương trình $4^{f(x)}-(m-1)2^{f(x)+1}+2m-3=0$ có đúng ba nghiệm là
| $2020$ | |
| $2019$ | |
| $2021$ | |
| $2022$ |
Chọn phương án C.
$\begin{array}{lll}
&4^{f(x)}-(m-1)2^{f(x)+1}+2m-3&=0\\
\Leftrightarrow&\big(2^{f(x)}\big)^2-2(m-1)2^{f(x)}+2m-3&=0\\
\Leftrightarrow&\big(2^{f(x)}\big)^2+(2-2m)2^{f(x)}+2m-3&=0\\
\Leftrightarrow&\left[\begin{array}{l}2^{f(x)}=1\\ 2^{f(x)}=2m-3\end{array}\right.&\\
\Leftrightarrow&\left[\begin{array}{ll}f(x)=0&(1)\\ f(x)=\log_2(2m-3)&(2)\end{array}\right.&
\end{array}$
Dựa vào đồ thị $f(x)$ ta thấy phương trình (1) có $3$ nghiệm phân biệt. Vậy để phương trình đã cho có đúng $3$ nghiệm thì phương trình (2) thỏa mãn một trong hai trường hợp sau:
- Trường hợp 1: (2) vô nghiệm.
Vì $f(x)$ là hàm bậc $3$ nên phương trình $f(x)=t$ luôn có nghiệm với mọi $t$. Do đó, để (2) vô nghiệm thì $\log_2(2m-3)$ không xác định, tức là $2m-3\leq0$, hay $m\leq\dfrac{3}{2}$ (3). - Trường hợp 2: (2) và (1) có cùng tập nghiệm, tức là $\log_2(2m-3)=0\Leftrightarrow2m-3=1\Leftrightarrow m=2$ (4).
Từ (3) và (4) suy ra $m\in\big\{-2018;-2017;\ldots;0;1;2\big\}$, tức là có $2021$ số nguyên $m$ thỏa đề.
