Cho hai cây cột có chiều cao lần lượt là $6$m, $15$m và đặt cách nhau $20$m (như hình minh họa).
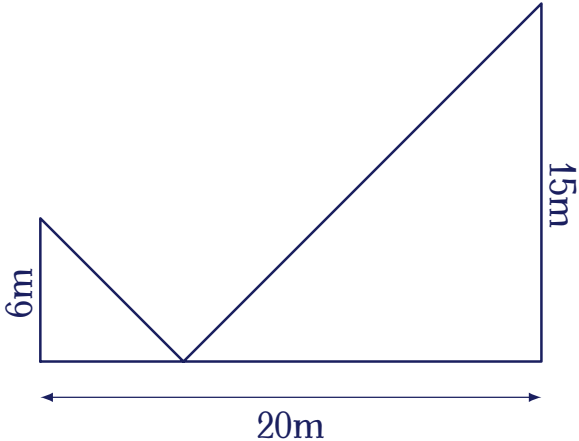
Một sợi dây dài được gắn vào đỉnh của mỗi cột và được đóng cọc xuống đất tại một điểm ở giữa hai cột. Chiều dài sợi dây được sử dụng ít nhất là
| $30$m | |
| $29$m | |
| $31$m | |
| $28$m |
Chọn phương án B.
Gọi A, B, C, D, M là các điểm như hình vẽ. Khi đó, chiều dài sợi dây là độ dài đường gấp khúc $CMD$.

Ta có $CM+MD=C'M+MD$.
Dấu "=" xảy ra khi $C',\,M,\,D$ thẳng hàng (như hình vẽ).
Đặt $x=AM$ ($0<x<20$).
Vì hai tam giác $AC'M$ và $BDM$ đồng dạng nên $$\begin{aligned}
\dfrac{AM}{BM}=\dfrac{AC'}{BD}&\Leftrightarrow\dfrac{x}{20-x}=\dfrac{6}{15}=\dfrac{2}{5}\\
&\Leftrightarrow5x=2(20-x)\\
&\Leftrightarrow x=\dfrac{40}{7}
\end{aligned}$$
Khi đó $CM+DM=\sqrt{6^2+x^2}+\sqrt{15^2+(20-x)^2}=29$m.
Vậy giá trị nhỏ nhất của $f(x)$ trên đoạn $[0;20]$ là $29$.
Chọn phương án B.
Gọi A, B, C, D, M là các điểm như hình vẽ. Khi đó, chiều dài sợi dây là độ dài đường gấp khúc $CMD$.
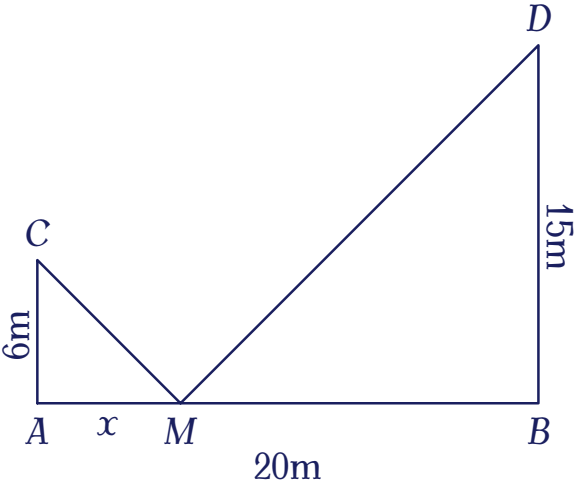
Gọi $x=AM$ ($0\leq x\leq20$). Ta có:
- $CM=\sqrt{CA^2+AM^2}=\sqrt{6^2+x^2}$
- $DM=\sqrt{DB^2+BM^2}=\sqrt{15^2+(20-x)^2}$
Suy ra $CM+MD=\sqrt{6^2+x^2}+\sqrt{15^2+(20-x)^2}$.
Xét $f(x)=\sqrt{6^2+x^2}+\sqrt{15^2+(20-x)^2}$ trên đoạn $[0;20]$ ta có $$f'(x)=\dfrac{x}{\sqrt{6^2+x^2}}+\dfrac{x-20}{\sqrt{15^2+(20-x)^2}}.$$
Cho $f'(x)=0\Leftrightarrow x=\dfrac{40}{7}$.
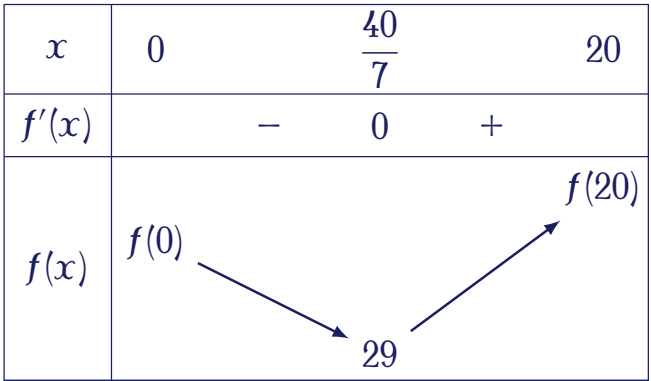
Vậy giá trị nhỏ nhất của $f(x)$ trên đoạn $[0;20]$ là $29$m.
