Ngân hàng bài tập
A
Với $\log3=a$ và $\log5=b$ thì $\log_945$ biểu diễn theo $a,\,b$ là
| $\dfrac{2a+b}{2a}$ | |
| $\dfrac{4a+b}{2a}$ | |
| $\dfrac{a+2b}{2a}$ | |
| $\dfrac{a+b}{a}$ |
2 lời giải
Chọn phương án A.
Sử dụng máy tính cầm tay:
- Lần lượt lưu giá trị $\log3$ và $\log5$ vào biến nhớ A, B:


- Tính giá trị $\log_945$ và so sánh với các phương án A, B, C, D:
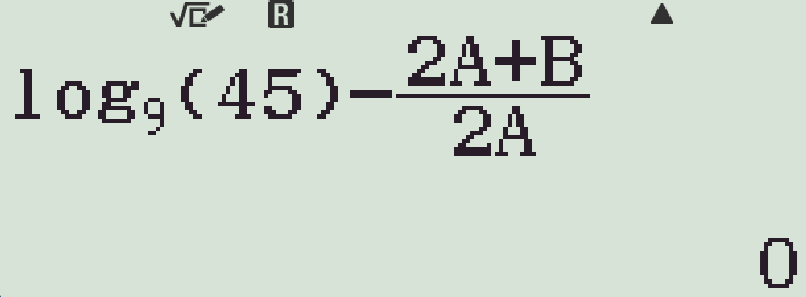
Chọn phương án A.
$\begin{aligned}
\log_945&=\dfrac{\log45}{\log9}=\dfrac{\log(9\cdot5)}{\log9}\\
&=\dfrac{\log9+\log5}{\log9}=\dfrac{\log3^2+\log5}{\log3^2}\\
&=\dfrac{2\log3+\log5}{2\log3}=\dfrac{2a+b}{2a}.
\end{aligned}$
