Ngân hàng bài tập
B
Giá trị cực tiểu của hàm số $y=x^4-4x^2+3$ là
| $y_{\text{CT}}=0$ | |
| $y_{\text{CT}}=3$ | |
| $y_{\text{CT}}=\sqrt{2}$ | |
| $y_{\text{CT}}=-1$ |
1 lời giải
Chọn phương án D.
Ta có $y'=4x^3-8x=4x\big(x^2-2\big)$.
Cho $y'=0\Leftrightarrow\left[\begin{array}{l}x=0\\ x=\pm\sqrt{2}\end{array}\right.$
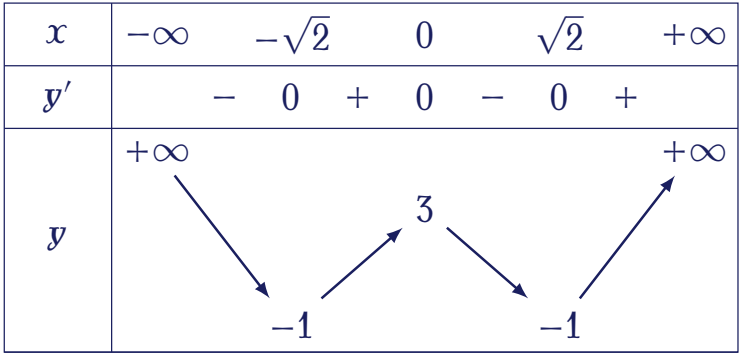
Vậy giá trị cực tiểu $y_{\text{CT}}=-1$.
