Ngân hàng bài tập
A
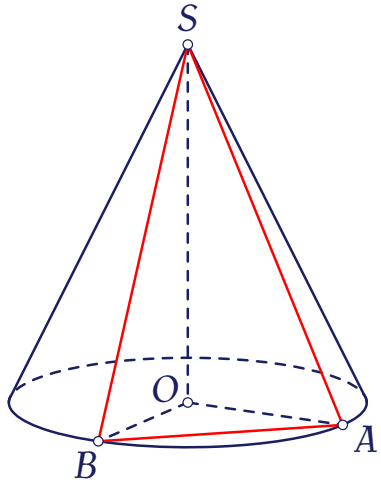
Cho hình nón đỉnh $S$ có đường cao bằng $6$cm, bán kính đáy bằng $10$cm. Trên đường tròn đáy lấy hai điểm $A,\,B$ sao cho $AB=12$cm. Diện tích tam giác $SAB$ bằng bao nhiêu?
| $60\text{ cm}^2$ | |
| $40\text{ cm}^2$ | |
| $48\text{ cm}^2$ | |
| $100\text{ cm}^2$ |
1 lời giải
Chọn phương án A.
Tam giác $SAB$ cân tại $S$, có $AB=12$ và $SA=SB=\ell=\sqrt{6^2+10^2}=2\sqrt{34}$.
Nửa chu vi: $p=\dfrac{AB+SA+SB}{2}=6+2\sqrt{34}$.
Theo công thức Heron ta có $$S=\sqrt{p(p-AB)(p-SA)(p-SB)}=60.$$
