Ngân hàng bài tập
A
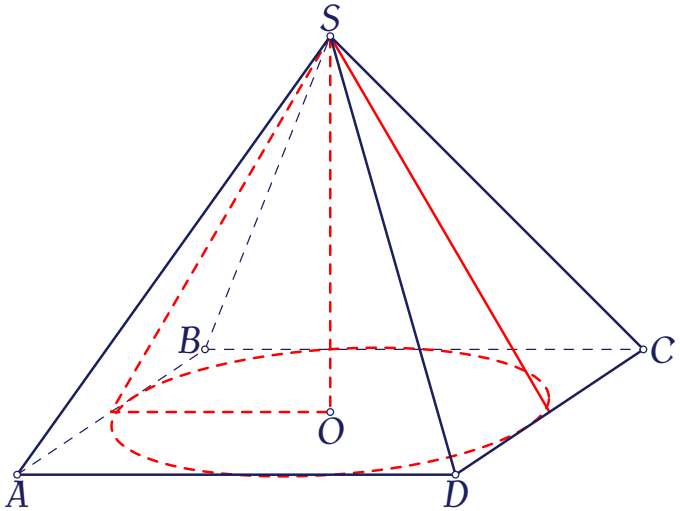
Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng $a$ và chiều cao bằng $2a$, diện tích xung quanh của hình nón đỉnh $S$ và đáy là hình tròn nội tiếp $ABCD$ bằng
| $\dfrac{\pi a^2\sqrt{17}}{8}$ | |
| $\dfrac{\pi a^2\sqrt{15}}{4}$ | |
| $\dfrac{\pi a^2\sqrt{17}}{4}$ | |
| $\dfrac{\pi a^2\sqrt{17}}{6}$ |
1 lời giải
Chọn phương án C.
Hình nón có chiều cao $h=2a$, bán kính đáy $r=\dfrac{a}{2}$.
Suy ra đường sinh $\ell=\sqrt{(2a)^2+\left(\dfrac{a}{2}\right)^2}=\dfrac{a\sqrt{17}}{2}$.
Vậy diện tích $S_{\text{xq}}=\pi r\ell=\pi\cdot\dfrac{a}{2}\cdot\dfrac{a\sqrt{17}}{2}=\dfrac{\pi a^2\sqrt{17}}{4}$.
