Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $A$, $\widehat{ABC}=30^\circ$. Tam giác $SBC$ là tam giác đều cạnh $a$ và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối chóp $S.ABC$ là
| $\dfrac{3a^3}{16}$ | |
| $\dfrac{a^3}{16}$ | |
| $\dfrac{a^3\sqrt{3}}{16}$ | |
| $\dfrac{3\sqrt{3}a^3}{16}$ |
Chọn phương án B.
Trong tam giác vuông $ABC$ ta có $$\begin{aligned}
\cos\widehat{ABC}=\dfrac{BA}{BC}\Rightarrow BA&=BC\cdot\cos\widehat{ABC}\\ &=a\cdot\cos30^\circ=\dfrac{a\sqrt{3}}{2}.
\end{aligned}$$
Khi đó $\begin{aligned}[t]
S_{ABC}&=\dfrac{1}{2}BA\cdot BC\cdot\sin\widehat{ABC}\\ &=\dfrac{1}{2}\cdot\dfrac{a\sqrt{3}}{2}\cdot a\cdot\sin30^\circ\\ &=\dfrac{a^2\sqrt{3}}{8}.
\end{aligned}$
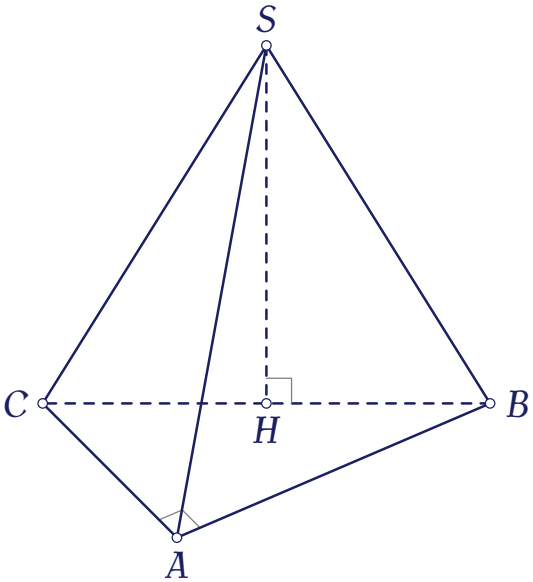
Gọi $H$ là trung điểm cạnh $BC$, ta có $SH=a\cdot\dfrac{\sqrt{3}}{2}$.
Vì $(SBC)\perp(ABC)$ và $SH\perp BC$ nên $SH\perp(ABC)$.
Vậy $V_{S.ABC}=\dfrac{1}{3}\cdot S_{ABC}\cdot SH=\dfrac{1}{3}\cdot\dfrac{a^2\sqrt{3}}{8}\cdot\dfrac{a\sqrt{3}}{2}=\dfrac{a^3}{16}$.
