Ngân hàng bài tập
A
Cho tam giác \(ABC\) có \(AB=3\), \(AC=4\) và \(\tan A=2\sqrt{2}\). Tính cạnh \(BC\).
| \(\sqrt{13}\) | |
| \(3\sqrt{2}\) | |
| \(4\sqrt{2}\) | |
| \(\sqrt{17}\) |
2 lời giải
Chọn phương án D.
Dùng máy tính cầm tay:
- Bấm ql\(2\sqrt{2}\)=
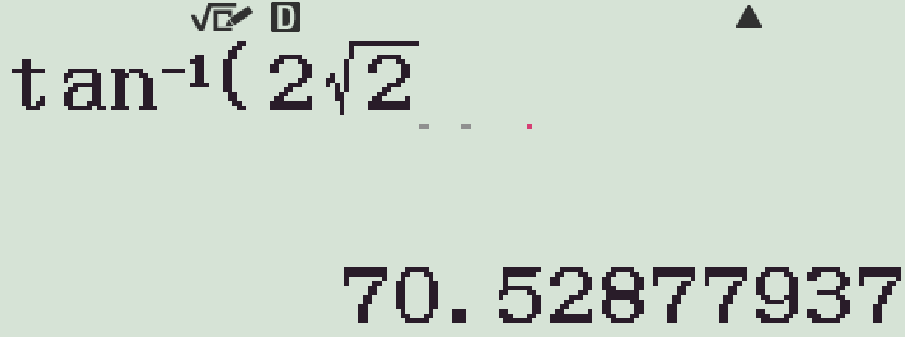
- Bấm s\(3^2\)+\(4^2\)p\(2\)O\(3\)O\(4\)OkM)=
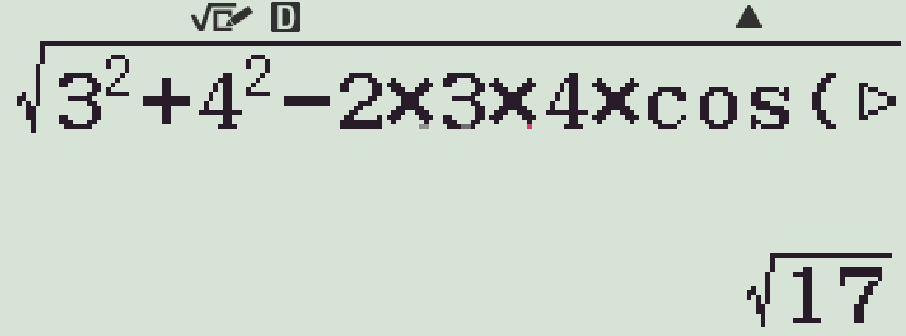
Chọn phương án D.
Ta có \(\dfrac{1}{\cos^2A}=1+\tan^2A=1+\left(2\sqrt{2}\right)^2=9\).
Suy ra \(\cos^2A=\dfrac{1}{9}\).
Vì \(\tan A=2\sqrt{2}>0\) nên \(A\) là góc nhọn, do đó \(\cos A=\dfrac{1}{3}>0\).
Khi đó, $$\begin{aligned}
BC&=\sqrt{AB^2+AC^2-2\cdot AB\cdot AC\cos A}\\
&=\sqrt{3^2+4^2-2\cdot3\cdot4\cdot\dfrac{1}{3}}\\
&=\sqrt{17}.
\end{aligned}$$
