Ngân hàng bài tập
A
Cho biểu thức \(f(x)=(2x-1)\left(x^3-1\right)\). Tập hợp tất cả các giá trị của \(x\) để \(f(x)\geq0\) là
| \(\left[\dfrac{1}{2};1\right]\) | |
| \(\left(-\infty;-\dfrac{1}{2}\right)\cup(1;+\infty)\) | |
| \(\left(-\infty;\dfrac{1}{2}\right]\cup[1;+\infty)\) | |
| \(\left(\dfrac{1}{2};1\right)\) |
1 lời giải
Chọn phương án C.
Ta có \(f(x)=(2x-1)(x-1)\left(x^2+x+1\right)\).
Bảng xét dấu: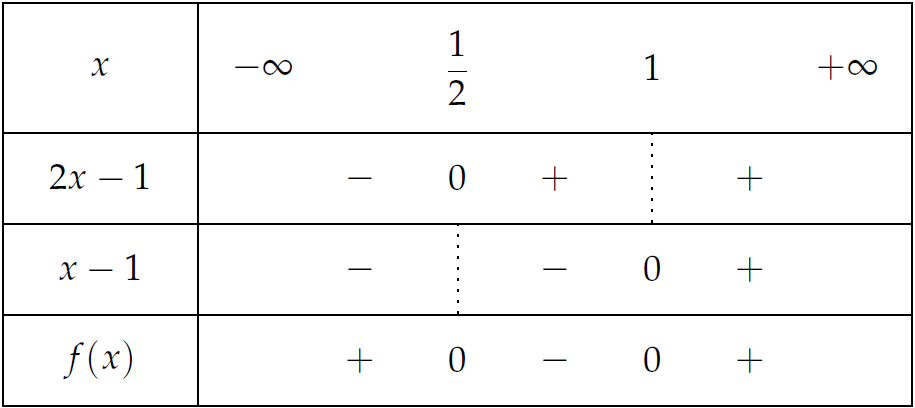
Theo đó, \(f(x)\geq0\Leftrightarrow x\in\left(-\infty;\dfrac{1}{2}\right]\cup[1;+\infty)\).
