Ngân hàng bài tập
A
Cho biểu thức \(f(x)=\dfrac{-4}{3x+1}-\dfrac{3}{2-x}\). Tìm tập hợp tất cả các giá trị của \(x\) sao cho \(f(x)>0\).
| \(\left(-\dfrac{11}{5};-\dfrac{1}{3}\right)\cup[2;+\infty)\) | |
| \(\left(-\dfrac{11}{5};-\dfrac{1}{3}\right)\cup(2;+\infty)\) | |
| \(\left(-\infty;-\dfrac{11}{5}\right]\cup\left(-\dfrac{1}{3};2\right)\) | |
| \(\left(-\infty;-\dfrac{11}{5}\right)\cup\left(-\dfrac{1}{3};2\right)\) |
1 lời giải
Chọn phương án B.
\(\begin{aligned}f(x)&=\dfrac{-4(2-x)-3(3x+1)}{(3x+1)(2-x)}\\
&=\dfrac{-5x-11}{(3x+1)(2-x)}.\end{aligned}\)
Bảng xét dấu: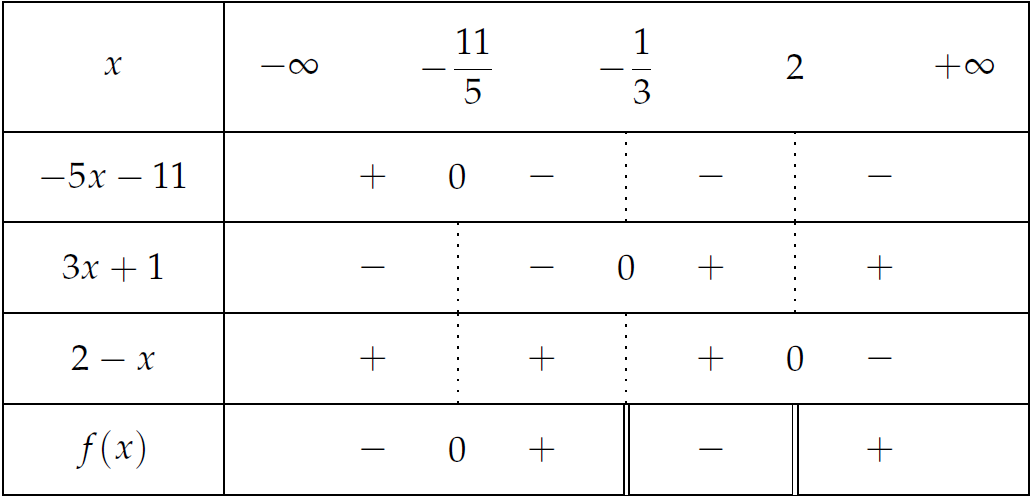
Vậy, \(f(x)>0\Leftrightarrow x\in\left(-\dfrac{11}{5};-\dfrac{1}{3}\right)\cup(2;+\infty)\).
