Ngân hàng bài tập
A
Một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt của một hình lập phương cạnh \(a\). Tính thể tích của khối trụ đã cho.
| \(V=\dfrac{\pi a^3}{12}\) | |
| \(V=\dfrac{\pi a^3}{6}\) | |
| \(V=\dfrac{\pi a^3}{2}\) | |
| \(V=\dfrac{\pi a^3}{4}\) |
1 lời giải
Chọn phương án D.
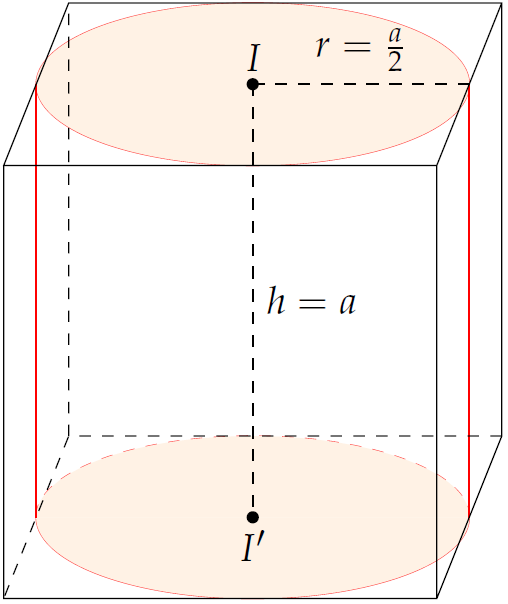
Mặt đáy của hình trụ là hình tròn nội tiếp hình vuông cạnh \(a\) nên có đường kính bằng \(a\). Vậy bán kính \(r=\dfrac{a}{2}\).
Đường cao của hình trụ bằng chiều dài cạnh của hình lập phương. Vậy \(h=a\).
Do đó \(V=\pi r^2\cdot h=\dfrac{\pi a^3}{4}\).
