Ngân hàng bài tập
A
Cho hình chữ nhật \(ABCD\) có \(AB=a\), \(BC=b\). Gọi \(M,\,N\) lần lượt là trung điểm của \(AB\) và \(CD\). Tính thể tích khối trụ thu được khi quay hình chữ nhật \(ABCD\) quanh trục \(MN\).
| \(V=\dfrac{\pi a^2b}{4}\) | |
| \(V=\pi a^2b\) | |
| \(V=\dfrac{\pi a^2b}{12}\) | |
| \(V=\dfrac{\pi a^2b}{3}\) |
1 lời giải
Chọn phương án A.
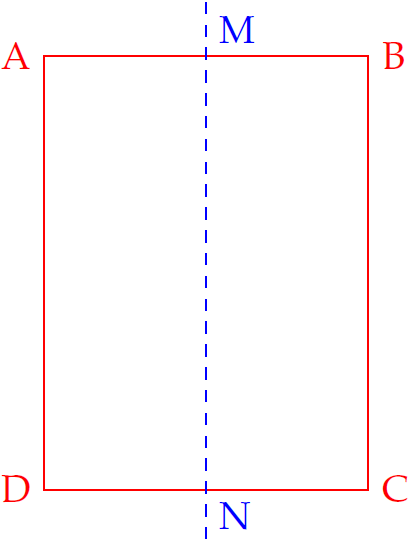
Hình trụ thu được có bán kính đáy \(r=\dfrac{AB}{2}=\dfrac{a}{2}\) và chiều cao \(h=BC=b\).
Vậy \(V=\pi r^2h=\dfrac{\pi a^2b}{4}\).
