Ngân hàng bài tập
A
Cắt một hình trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh bằng \(3a\). Tính diện tích toàn phần của hình trụ đã cho.
| \(S_{\text{tp}}=\dfrac{9\pi a^2}{2}\) | |
| \(S_{\text{tp}}=\dfrac{13\pi a^2}{6}\) | |
| \(S_{\text{tp}}=9\pi a^2\) | |
| \(S_{\text{tp}}=\dfrac{27\pi a^2}{2}\) |
1 lời giải
Chọn phương án D.
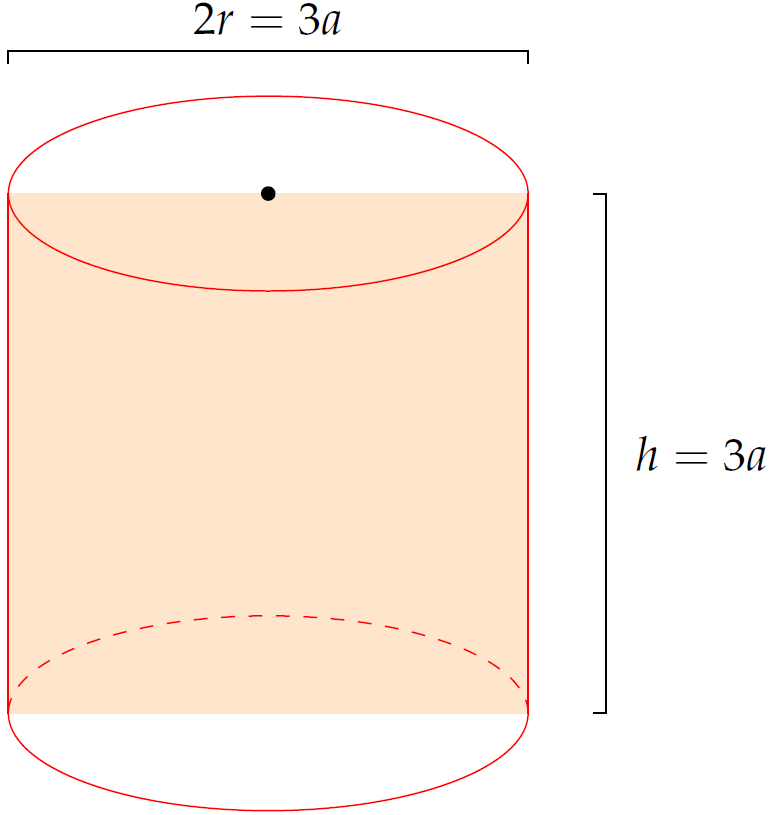
Vì thiết diện là hình vuông cạnh \(3a\) nên ta có:
- \(h=3a\).
- \(2r=3a\Leftrightarrow r=\dfrac{3a}{2}\).
Khi đó $$\begin{aligned}S_{\text{tp}}&=S_{\text{xq}}+2\left(\pi r^2\right)\\
&=2\pi rh+2\pi r^2\\
&=2\pi\cdot\dfrac{3a}{2}\cdot3a+2\pi\cdot\left(\dfrac{3a}{2}\right)^2\\
&=\dfrac{27\pi a^2}{2}.\end{aligned}$$
