Ngân hàng bài tập
S
Cho hình nón có diện tích xung quanh bằng \(3\pi a^2\) và bán kính đáy bằng \(a\). Tính tan của góc giữa một đường sinh và mặt đáy của hình nón.
| \(8\) | |
| \(2\sqrt{2}\) | |
| \(\dfrac{2\sqrt{2}}{3}\) | |
| \(\dfrac{1}{3}\) |
1 lời giải
Chọn phương án B.
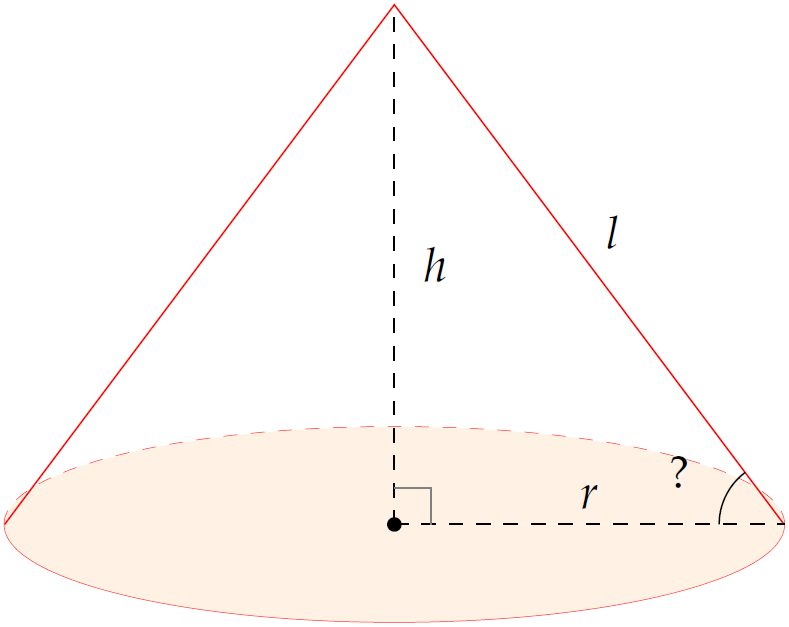
Ta có \(S_{\text{xq}}=\pi r l\).
Suy ra \(l=\dfrac{S_{\text{xq}}}{\pi r}=\dfrac{3\pi a^2}{\pi a}=3a\).
Khi đó, chiều cao \(h=\sqrt{l^2-r^2}=2a\sqrt{2}\).
Gọi \(\alpha\) là góc giữa một đường sinh và mặt đáy của hình nón. Ta có $$\tan\alpha=\dfrac{h}{r}=\dfrac{2a\sqrt{2}}{a}=2\sqrt{2}.$$
