Kết quả viết dưới dạng lũy thừa với số mũ hữu tỉ của biểu thức \(F=\dfrac{\sqrt{a\sqrt{a\sqrt{a\sqrt{a}}}}}{a^{\tfrac{11}{16}}}\) với \(a>0\) là
| \(F=a^{\tfrac{1}{4}}\) | |
| \(F=a^{\tfrac{3}{8}}\) | |
| \(F=a^{\tfrac{1}{2}}\) | |
| \(F=a^{\tfrac{3}{4}}\) |
Chọn phương án A.
Dùng máy tính cầm tay:
- r \(a=2\) ta được \(A=2^n\approx1,1892\ldots\)
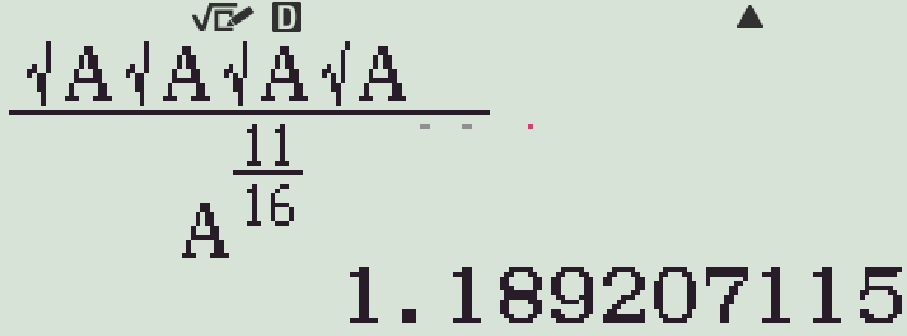
- Lấy logarit cơ số \(2\) hai vế ta được \(n=\log_2(\)M\()=\dfrac{1}{4}\)
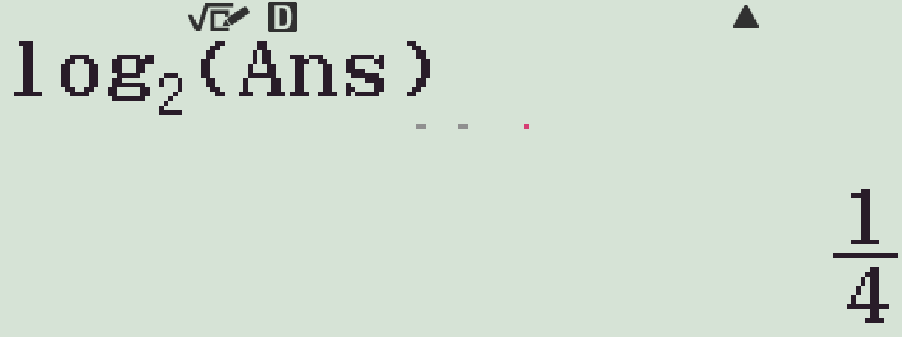
Vậy \(A=a^{\tfrac{1}{4}}\).
Chọn phương án A.
\(\begin{aligned}
F&=\dfrac{\sqrt{a\sqrt{a\sqrt{a\sqrt{a}}}}}{a^{\tfrac{11}{16}}}=\dfrac{\sqrt{a\sqrt{a\sqrt{a\cdot a^{\tfrac{1}{2}}}}}}{a^{\tfrac{11}{16}}}\\
&=\dfrac{\sqrt{a\sqrt{a\sqrt{a^{\tfrac{3}{2}}}}}}{a^{\tfrac{11}{16}}}=\dfrac{\sqrt{a\sqrt{a\cdot a^{\tfrac{3}{4}}}}}{a^{\tfrac{11}{16}}}\\
&=\dfrac{\sqrt{a\sqrt{a^{\tfrac{7}{4}}}}}{a^{\tfrac{11}{16}}}=\dfrac{\sqrt{a\cdot a^{\tfrac{7}{8}}}}{a^{\tfrac{11}{16}}}\\
&=\dfrac{\sqrt{a^{\tfrac{15}{8}}}}{a^{\tfrac{11}{16}}}=\dfrac{a^{\tfrac{15}{16}}}{a^{\tfrac{11}{16}}}\\
&=a^{\tfrac{15}{16}-\tfrac{11}{16}}=a^{\tfrac{1}{4}}.
\end{aligned}\)
