Ngân hàng bài tập
A
Rút gọn biểu thức \(A=\dfrac{\sqrt[3]{a^7}\cdot a^{\tfrac{11}{3}}}{a^4\cdot\sqrt[7]{a^{-5}}}\) với \(a>0\) ta được kết quả \(A=a^{\tfrac{m}{n}}\) trong đó \(m,\,n\in\Bbb{N}^*\) và \(\dfrac{m}{n}\) là phân số tối giản. Khẳng định nào sau đây đúng?
| \(m^2-n^2=312\) | |
| \(m^2+n^2=543\) | |
| \(m^2-n^2=-312\) | |
| \(m^2+n^2=409\) |
2 lời giải
Chọn phương án A.
Dùng máy tính cầm tay:
- r \(a=2\) ta được \(A=2^{\tfrac{m}{n}}\approx6,5626\ldots\)
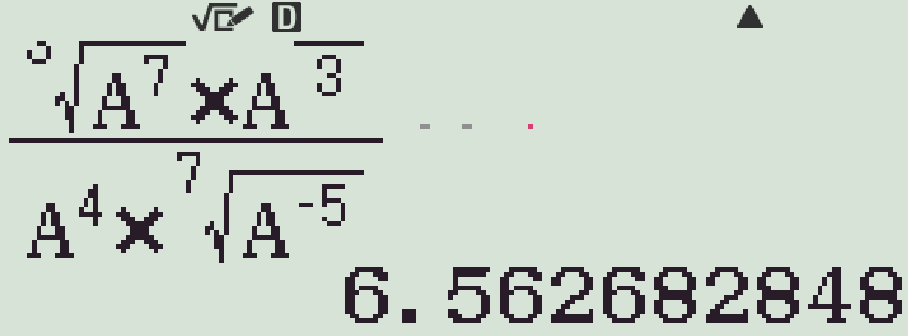
- Lấy logarit cơ số \(2\) hai vế ta được \(\dfrac{m}{n}=\log_2(\)M\()=\dfrac{19}{7}\).

Vậy \(m=19\), \(n=7\).
Suy ra \(m^2-n^2=312\).
Chọn phương án A.
Ta có \(A=\dfrac{a^{\tfrac{7}{3}}\cdot a^{\tfrac{11}{3}}}{a^4\cdot a^{-\tfrac{5}{7}}}=\dfrac{a^{\tfrac{7}{3}+\tfrac{11}{3}}}{a^{4-\tfrac{5}{7}}}=a^{\tfrac{19}{7}}\).
Vậy \(m=19\), \(n=7\).
Suy ra \(m^2-n^2=312\).
