Ngân hàng bài tập
B
Cho \(a,\,b\) là các số thực dương. Rút gọn \(P=\dfrac{a^{\tfrac{4}{3}}b+ab^{\tfrac{4}{3}}}{\sqrt[3]{a}+\sqrt[3]{b}}\) ta được
| \(P=ab\) | |
| \(P=a+b\) | |
| \(P=a^4b+ab^4\) | |
| \(P=a^2b+ab^2\) |
2 lời giải
Chọn phương án A.
Dùng máy tính cầm tay:
- r \(a=2\), \(b=3\) ta được \(P=6\)
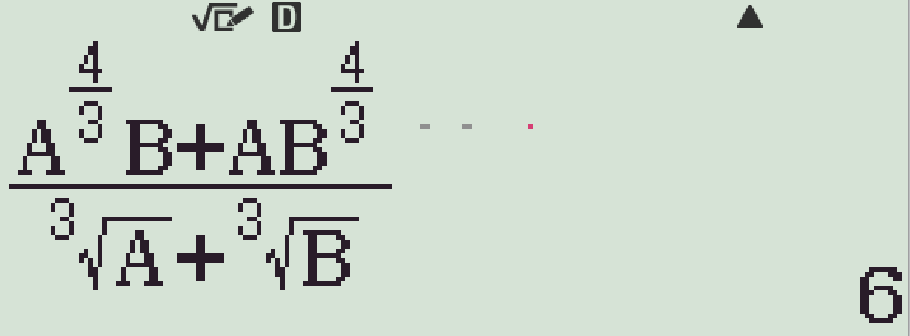
- Trong khi đó:
- \(ab=2\cdot3=6\)
- \(a+b=2+3=5\)
- \(a^4b+ab^4=210\)
- \(a^2b+ab^2=30\)
Vậy \(P=ab\).
Chọn phương án A.
\(\begin{aligned}
P&=\dfrac{a^{\tfrac{4}{3}}b+ab^{\tfrac{4}{3}}}{\sqrt[3]{a}+\sqrt[3]{b}}=\dfrac{a\cdot a^{\tfrac{1}{3}}b+ab\cdot b^{\tfrac{1}{3}}}{a^{\tfrac{1}{3}}+b^{\tfrac{1}{3}}}\\
&=\dfrac{ab\left(a^{\tfrac{1}{3}}+b^{\tfrac{1}{3}}\right)}{a^{\tfrac{1}{3}}+b^{\tfrac{1}{3}}}=ab.
\end{aligned}\)
