Tìm đạo hàm của hàm số \(y=\dfrac{\mathrm{e}^x+\mathrm{e}^{-x}}{\mathrm{e}^x-\mathrm{e}^{-x}}\).
| \(y'=\dfrac{\mathrm{e}^x}{\left(\mathrm{e}^x-\mathrm{e}^{-x}\right)^2}\) | |
| \(y'=\dfrac{-4}{\left(\mathrm{e}^x-\mathrm{e}^{-x}\right)^2}\) | |
| \(y'=\dfrac{-5}{\left(\mathrm{e}^x-\mathrm{e}^{-x}\right)^2}\) | |
| \(y'=\mathrm{e}^x+\mathrm{e}^{-x}\) |
Chọn phương án B.
Dùng máy tính cầm tay:
- Dùng chức năng qy ta tính được \(y'(2)\approx-0,07602\ldots\)
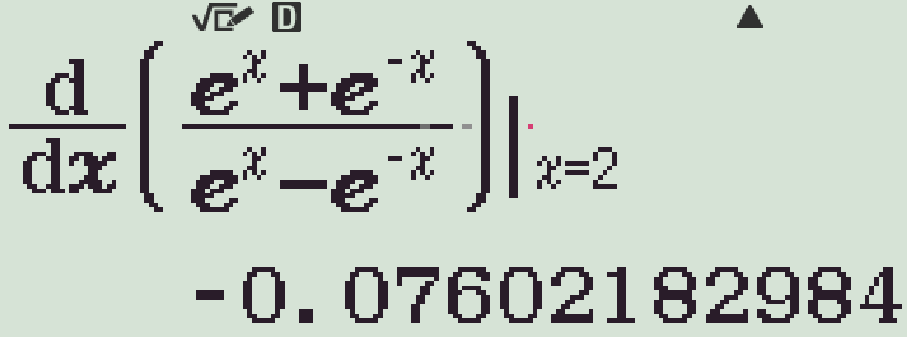
- r \(x=2\) từng phương án ta tìm được \(y'=\dfrac{-4}{\left(\mathrm{e}^x-\mathrm{e}^{-x}\right)^2}\).
Chọn phương án B.
\(\begin{aligned}
y'&=\dfrac{\left(\mathrm{e}^x+\mathrm{e}^{-x}\right)'\left(\mathrm{e}^x-\mathrm{e}^{-x}\right)-\left(\mathrm{e}^x+\mathrm{e}^{-x}\right)\left(\mathrm{e}^x-\mathrm{e}^{-x}\right)'}{\left(\mathrm{e}^x-\mathrm{e}^{-x}\right)^2}\\
&=\dfrac{\left(\mathrm{e}^x-\mathrm{e}^{-x}\right)\left(\mathrm{e}^x-\mathrm{e}^{-x}\right)-\left(\mathrm{e}^x+\mathrm{e}^{-x}\right)\left(\mathrm{e}^x+\mathrm{e}^{-x}\right)}{\left(\mathrm{e}^x-\mathrm{e}^{-x}\right)^2}\\
&=\dfrac{\left(\mathrm{e}^{2x}-2+\mathrm{e}^{-2x}\right)-\left(\mathrm{e}^{2x}+2+\mathrm{e}^{-2x}\right)}{\left(\mathrm{e}^x-\mathrm{e}^{-x}\right)^2}\\
&=\dfrac{-4}{\left(\mathrm{e}^x-\mathrm{e}^{-x}\right)^2}.
\end{aligned}\)
