Ngân hàng bài tập
Tìm đạo hàm của hàm số \(y=\dfrac{x+1}{4^x}\).
| \(y'=\dfrac{1+2(x+1)\ln2}{2^{2x}}\) | |
| \(y'=\dfrac{1-2(x+1)\ln2}{2^{2x}}\) | |
| \(y'=\dfrac{1+2(x+1)\ln2}{2^{x^2}}\) | |
| \(y'=\dfrac{1-2(x+1)\ln2}{2^{x^2}}\) |
2 lời giải
Chọn phương án B.
Dùng máy tính cầm tay:
- Dùng chức năng qy ta tính được \(y'(2)\approx-0,19743\ldots\)
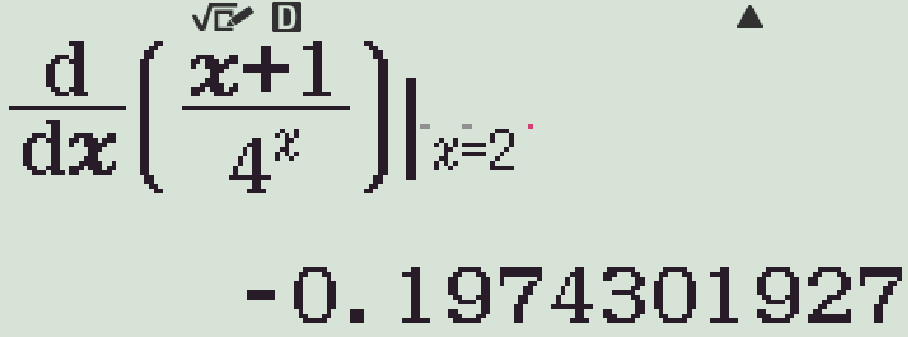
- r \(x=2\) từng phương án ta tìm được \(y'=\dfrac{1-2(x+1)\ln2}{2^{2x}}\).
Chọn phương án B.
\(\begin{aligned}
y'&=\dfrac{(x+1)'4^x-(x+1)\left(4^x\right)'}{\left(4^x\right)^2}\\
&=\dfrac{4^x-(x+1)4^x\ln4}{\left(4^x\right)^2}\\
&=\dfrac{4^x\left[1-(x+1)\ln4\right]}{\left(4^x\right)^2}\\
&=\dfrac{1-(x+1)\ln4}{4^x}\\
&=\dfrac{1-2(x+1)\ln2}{2^{2x}}.
\end{aligned}\)
$$\left(\dfrac{u}{v}\right)'=\dfrac{u'\cdot v-u\cdot v'}{v^2}$$
