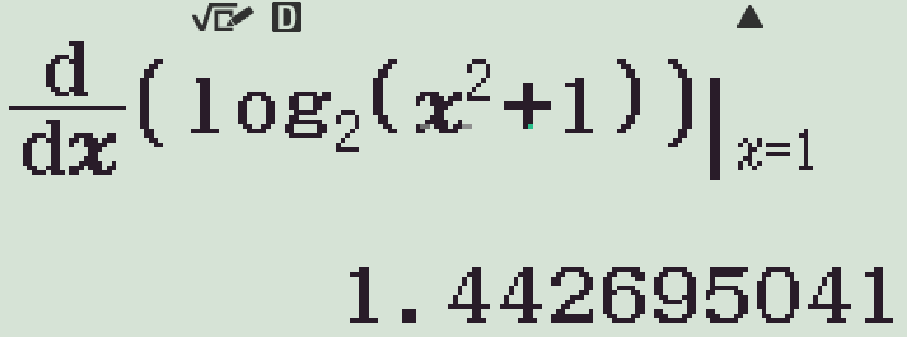Ngân hàng bài tập
Cho hàm số \(f(x)=\log_2\left(x^2+1\right)\). Tính \(f'(1)\).
| \(f'(1)=\dfrac{1}{\ln2}\) | |
| \(f'(1)=\dfrac{1}{2}\) | |
| \(f'(1)=\dfrac{1}{2\ln2}\) | |
| \(f'(1)=1\) |
1 lời giải
Chọn phương án A.
Ta có \(f'(x)=\dfrac{\left(x^2+1\right)'}{\left(x^2+1\right)\ln2}=\dfrac{2x}{\left(x^2+1\right)\ln2}\).
Khi đó, \(f'(1)=\dfrac{2\cdot1}{\left(1^2+1\right)\ln2}=\dfrac{1}{\ln2}\).