Ngân hàng bài tập
A
Cho tứ giác lồi \(ABCD\) có \(\widehat{ABC}=\widehat{ADC}=90^\circ\), \(\widehat{BAD}=120^\circ\) và \(BD=a\sqrt{3}\). Tính \(AC\).
| \(AC=2a\) | |
| \(AC=a\sqrt{3}\) | |
| \(AC=a\) | |
| \(AC=a\sqrt{5}\) |
1 lời giải
Chọn phương án A.
Theo đề bài ta có \(\widehat{ABC}=\widehat{ADC}=90^\circ\).
Suy ra tứ giác ABCD nội tiếp đường tròn đường kính \(AC\).
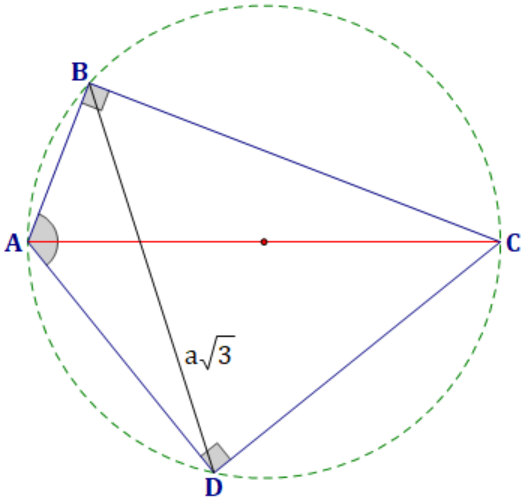
Áp dụng định lý sin cho tam giác \(ABD\) ta có $$\dfrac{BD}{\sin\widehat{BAD}}=2R\Rightarrow R=\dfrac{a\sqrt{3}}{2\sin120^\circ}=a.$$Do đó \(AC=2R=2a\).
