Ngân hàng bài tập
C
Cho lục giác đều \(ABCDEF\) có tâm \(O\).
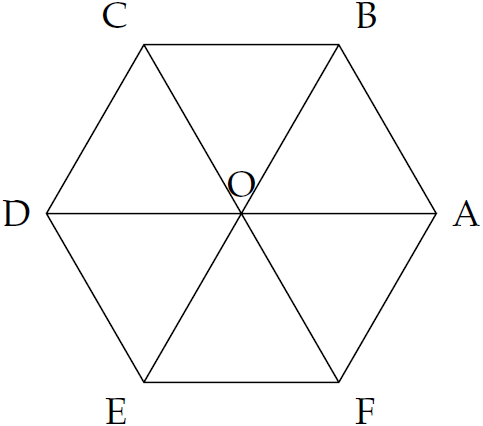
Có bao nhiêu vectơ (khác \(\vec{0}\)) ngược hướng với vectơ \(\overrightarrow{OB}\) mà có điểm đầu và điểm cuối là một trong các đỉnh và tâm của \(ABCDEF\)?
| \(3\) | |
| \(9\) | |
| \(5\) | |
| \(4\) |
1 lời giải
Chọn phương án C.
Các vectơ thỏa đề bao gồm \(\overrightarrow{BO}\), \(\overrightarrow{OE}\), \(\overrightarrow{CD}\), \(\overrightarrow{AF}\), \(\overrightarrow{BE}\).
Vậy có \(5\) vectơ.
