Ngân hàng bài tập
B
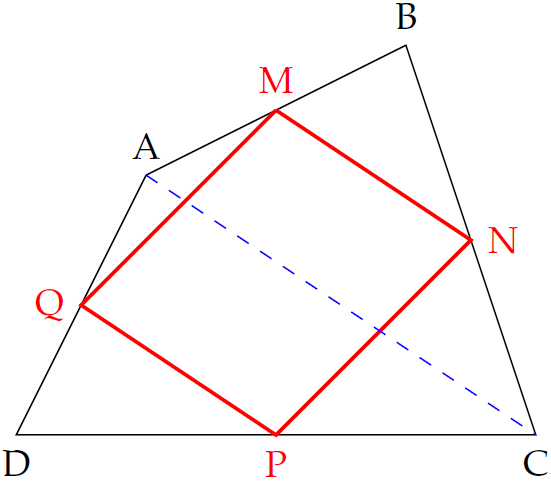
Cho tứ giác \(ABCD\). Gọi \(M,\,N,\,P,\,Q\) lần lượt là trung điểm của \(AB\), \(BC\), \(CD\), \(DA\). Khẳng định nào sau đây sai?
| \(\overrightarrow{MN}=\overrightarrow{QP}\) | |
| \(\left|\overrightarrow{QP}\right|=\left|\overrightarrow{MN}\right|\) | |
| \(\overrightarrow{MQ}=\overrightarrow{NP}\) | |
| \(\left|\overrightarrow{MN}\right|=\left|\overrightarrow{AC}\right|\) |
1 lời giải
Chọn phương án D.
♥ Tam giác \(ABC\) có \(MN\) là đường trung bình nên $$\begin{cases}
MN\parallel AC\\
MN=\dfrac{1}{2}AC
\end{cases}\quad(1)$$
♥ Tam giác \(ADC\) có \(PQ\) là đường trung bình nên $$\begin{cases}
PQ\parallel AC\\
PQ=\dfrac{1}{2}AC
\end{cases}\quad(2)$$
Từ (1) và (2) suy ra \(\begin{cases}
MN\parallel PQ\\
MN=PQ.
\end{cases}\)
Do đó \(MNPQ\) là hình bình hành, suy ra
- \(\overrightarrow{MN}=\overrightarrow{QP}\)
- \(\left|\overrightarrow{QP}\right|=\left|\overrightarrow{MN}\right|\)
- \(\overrightarrow{MQ}=\overrightarrow{NP}\)