Cho tam giác \(ABC\) có \(b=7\), \(c=5\), \(\cos A=\dfrac{3}{5}\). Đường cao \(h_a\) của tam giác \(ABC\) là
| \(8\) | |
| \(\dfrac{7\sqrt{2}}{2}\) | |
| \(80\sqrt{3}\) | |
| \(8\sqrt{3}\) |
Chọn phương án B.
Ta có thể tìm ra độ dài đường cao chỉ thông qua các bước bấm máy tính cầm tay.
Bước 1. Tính độ dài cạnh \(a\).
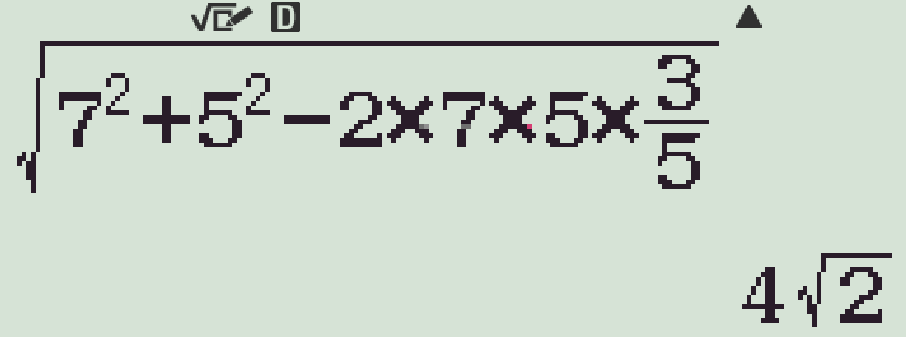
→ Lưu kết quả này vào biến nhớ A: qJz

Bước 2. Tính nửa chu vi \(p\).

→ Lưu kết quả này vào biến nhớ B: qJx

Bước 3. Tính diện tích \(S\).

Bước 4. Tính đường cao \(h_a\).

Chọn phương án B.
Theo định lý cosin ta có $$\begin{align*}
a^2&=b^2+c^2-2bc\cos A\\
&=7^2+5^2-2\cdot7\cdot5\cdot\dfrac{3}{5}=32\\
\Rightarrow a&=4\sqrt{2}.
\end{align*}$$
Suy ra \(S=\sqrt{p(p-a)(p-b)(p-c)}=14\).
Vì \(h_a\) là đường cao nên ta có \(S=\dfrac{1}{2}a\cdot h_a\).
\(\Rightarrow h_a=\dfrac{2S}{a}=\dfrac{2\cdot14}{4\sqrt{2}}=\dfrac{7\sqrt{2}}{2}\).
Chọn phương án B.
Theo định lý cosin ta có $$\begin{align*}
a^2&=b^2+c^2-2bc\cos A\\
&=7^2+5^2-2\cdot7\cdot5\cdot\dfrac{3}{5}=32\\
\Rightarrow a&=4\sqrt{2}.
\end{align*}$$
\Rightarrow\sin^2A&=1-\cos^2A=\dfrac{16}{25}\\
\Rightarrow\sin A&=\dfrac{4}{5}.\end{align*}$$
Suy ra \(S=\dfrac{1}{2}bc\sin A=\dfrac{1}{2}\cdot7\cdot5\cdot\dfrac{4}{5}=14\).
Vì \(h_a\) là đường cao nên ta có \(S=\dfrac{1}{2}a\cdot h_a\).
\(\Rightarrow h_a=\dfrac{2S}{a}=\dfrac{2\cdot14}{4\sqrt{2}}=\dfrac{7\sqrt{2}}{2}\).
