Ngân hàng bài tập
C
Cho hai hình bình hành \(ABCD\) và \(ABEF\) có chung cạnh \(AB\).
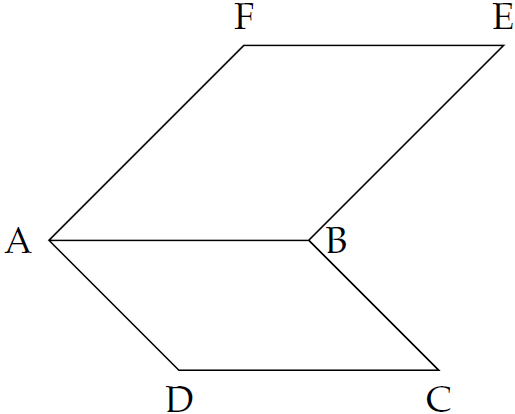
Vectơ nào sau đây bằng với vectơ \(\overrightarrow{CE}\)?
| \(\overrightarrow{AF}\) | |
| \(\overrightarrow{DF}\) | |
| \(\overrightarrow{BF}\) | |
| \(\overrightarrow{BD}\) |
1 lời giải
Chọn phương án B.
Tứ giác \(CDFE\) có cặp cạnh đối \(CD,\,FE\) song song và bằng nhau nên là hình bình hành.
Từ đó suy ra \(\overrightarrow{CE}=\overrightarrow{DF}\).
